Proceso de carga:
Cuando el interruptor se mueve a A, la corriente I sube
bruscamente (como un cortocircuito) y tiene el valor de I = E / R amperios
(como si el condensador no existiera momentáneamente en este circuito serie
RC), y poco a poco esta corriente va disminuyendo hasta tener un valor de cero
(ver el diagrama inferior).
El voltaje en el condensador no varía instantáneamente y
sube desde 0 voltios hasta E voltios (E es el valor de la fuente de corriente
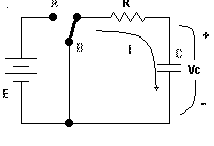
directa conectado en serie con R y C, ver diagrama 1).
El tiempo que se tarda el voltaje en el condensador (Vc) en
pasar de 0 voltios hasta el 63.2 % del voltaje de la fuente está dato por la
fórmula T = R x C donde R está en Ohmios y C en Milifaradios y el resultado
estará en milisegundos.
Después de 5 x T (5 veces T) el voltaje ha subido hasta un
99.3 % de su valor final
Al valor de T se le llama "Constante de tiempo"
Analizan los dos gráficos se puede ver que están divididos
en una parte transitoria y una parte estable. Los valores de Ic y Vc varían sus
valores en la parte transitoria (aproximadamente 5 veces la constante de tiempo
T), pero no así en la parte estable.
Los valores de Vc e Ic en cualquier momento se pueden
obtener con las siguientes fórmulas:
Vc = E + ( Vo - E) x e-T/ t ,
Vo es el voltaje inicial del condensador (en muchos casos
es 0 Voltios)
Ic = ( E - Vo ) x e-T/ t/ R
Vo es el voltaje inicial del condensador (en muchos casos
es 0 Voltios)
VR = E x e-T/ t Donde : T = R x C
Proceso de descarga:
El interruptor está en B.
Entonces el voltaje en el condensador Vc
empezará a descender desde Vo (voltaje inicial en el condensador). La corriente
tendrá un valor inicial de Vo / R y disminuirá hasta llegar a 0 (cero voltios).
Los valores de Vc e I en cualquier
momento se pueden obtener con las siguientes fórmulas:
Vc = Vo x e-t / T I = -(Vo / R) e-t / T
Donde: T = RC es la constante de tiempo
NOTA: Si el condensador había sido
previamente cargado hasta un valor E, hay que reemplazar Vo en las fórmulas con
E
Material extraido de: Electrónica Fácil












0 comentarios:
Publicar un comentario