Situamos imaginariamente, una superficie esférica concéntrica de
radio r, para determinar el campo eléctrico en las distintas regiones aplicando
la ley de Gauss. Como ya se ha explicado en
la página titulada “Modelo atómico de Kelvin_Thomson”, en este problema de
simetría esférica, el campo eléctrico tiene dirección radial y su módulo es
constante en todos los puntos de una superficie esférica de radio r. El flujo
del campo eléctrico E a través de dicha superficie cerrada vale
Determinamos la carga q encerrada en dicha superficie
esférica, para distintos valores del radio r, aplicamos la
ley de Gauss
Para r<a, la superficie esférica de radio r, no contiene ninguna carga, q=0, y E=0
Para a<r<b, la superficie esférica de radio r, contiene una carga, q=+Q,
Para r>b, la superficie esférica de radio r, contiene una carga, q=+Q-Q=0, y E=0
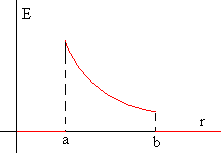 |
En la figura, se representa el módulo del campo E en función de r.
La diferencia de potencial entre las dos placas es de radios a y b es
|
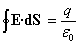

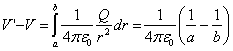










CASINO - JAMUARY 2019 - JAMUARY 2019
ResponderBorrarJAMUARY 2019. CASINO - JAMUARY 이천 출장안마 2019. JAMUARY 2019. CASINO - JAMUARY 2019. JAMUARY 2019. 동해 출장마사지 JAMUARY 양산 출장샵 2019. JAMUARY 2019. JAMUARY 2019. JAMUARY 2019. 부천 출장안마 JAMUARY 2019. JAMUARY 대구광역 출장안마 2019. JAMUARY